Symmetrie und Schiefe
Um eine metrische Verteilung charakterisieren zu können, ist neben der zentralen Lage- und Streuung auch deren Symmetrie und Schiefe von Bedeutung. Die Symmetrie sagt etwas über die (Un-)Gleichverteilung der Werte einer Variablen aus. Bei stark asymmetrischen Variablen (z.B. Haushaltseinkommen in Deutschland) ist das auftreten von kleinen Werten viel wahrscheinlicher, als das auftreten von sehr großen Werten (oder umgekehrt). Das Bild zeigt Histogramme für verschiedene simulierte Zufallswerte der Beta-Verteilung. Dabei wurden jeweils die Parameter der theoretischen Verteilung $\alpha$ und $\beta$ geändert. Somit kann eine große Bandbreite charakteristischer Verteilungen abgedeckt werden. Neben dem Histogramm wurde auch der empirische Median und Mittelwert der Verteilung als vertikale Linien eingezeichnet. Für symmetrische Verteilungen gilt, dass der Mittelwert und der Median gleich sind und das Histogramm an diesen Achsen gespiegelt werden kann. Eine linkssteile (rechtschiefe) Verteilung ergibt sich durch einige überdurchschnittlich große Werte. In diesem Fall ist der Mittelwert größer als der Median. Eine rechtssteile (linksschiefe) Verteilung ist durch einige unterdurchschnittlich kleine Werte geprägt. Hier ist der Median größer als der Mittelwert. Zudem kann eine Verteilung auch Gleichverteilt, Bi- oder Multimodal sein. Im ersten Fall gibt es keinen Modus, also keinen Wert der Verteilung, der am Häufigsten vorkommt. In den letzteren Fällen gibt es ein oder mehrere Modi. Im Histogramm sind multimodale Verteilungen daran zu erkennen, dass sie typischerweise über zwei oder mehr “Gipfel” verfügen. Mit dem folgenden Beispiel kannst Du ein Histogramm über die Anzahl der Ausleihen im Datensatz erstellen: Das Histogram zeigt, dass die Verteilung der Ausleihen durch einige sehr große Ausreißer geprägt ist. Der Mittelwert liegt hier bei $\bar{x} = 162$, während der Median $x_{0.5} = 19$ sehr viel kleiner ist. Das 95%-Quantil liegt bei $x_{0.95} = 816$ Ausleihen. Das heißt das 95% der Beobachtungen im Datensatz weniger als 816 Ausleihen getätigt haben.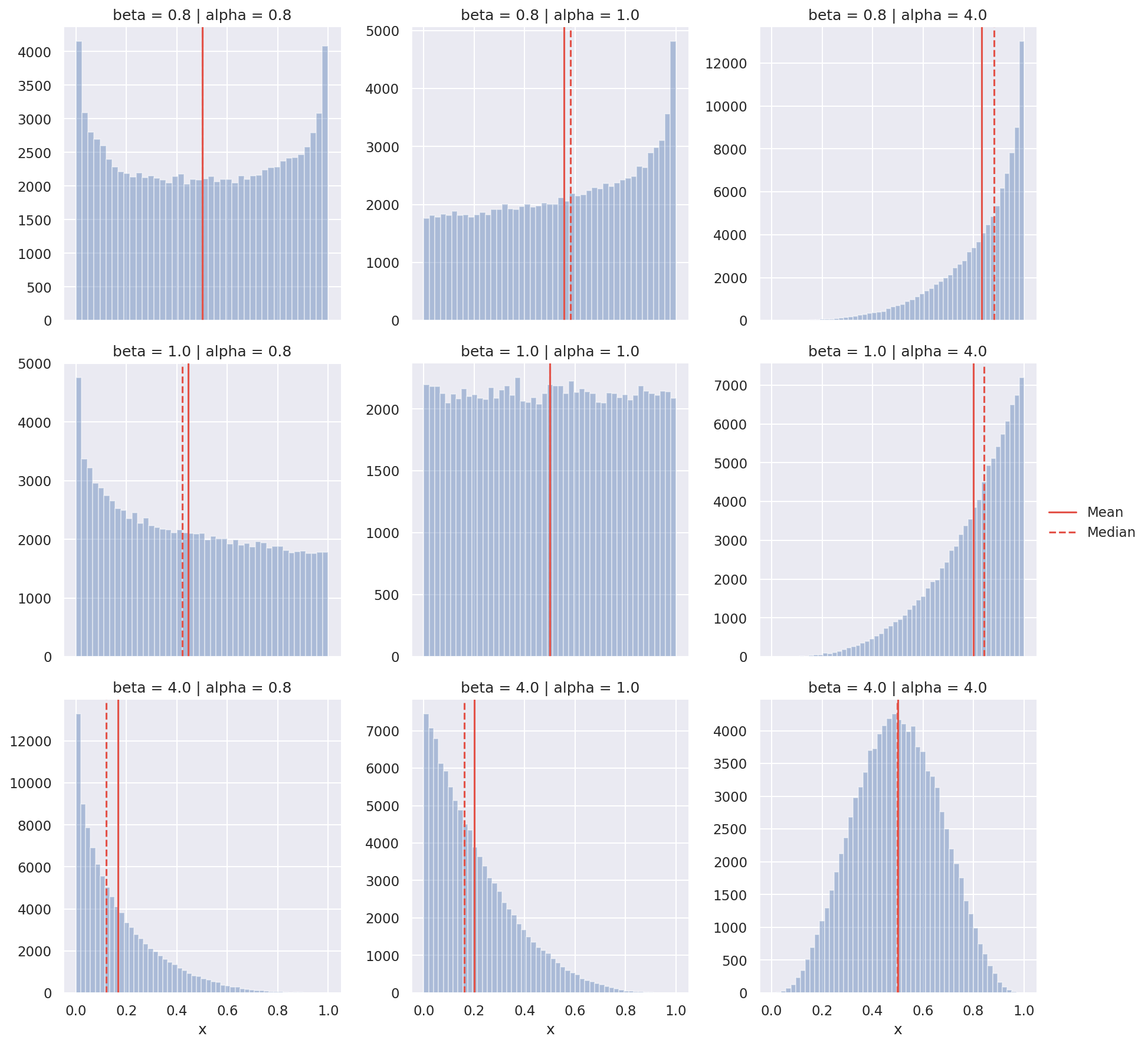
Verschiedene univariate Verteilungen
3.6 Symmetrie und Schiefe (15 Min)
Verteilung der Ausleihen pro Kunde
import pandas as pd
import seaborn as sns
%matplotlib inline
sns.set()
df = pd.read_csv("../data/Library_Usage.csv")
sns.distplot(df['Total Checkouts'], kde=False)
3.7 Exkurs: Ausreißerentfernung III (30 Min)
'Total Checkouts Sqrt', die die Wurzel über die Spalte Total Checkouts enthält. Die Wurzel für jede Beobachtung kannst Du mit df['Total Checkouts']**(0.5) berechnen.'Total Checkouts Sqrt' an und charakterisiere die Verteilung.